Estudiando la concavidad de una función es posible determinar si un punto crítico es un extremo local de dicha función. Intuitivamente, lo que ocurre es que al fijar un punto crítico de una función, si la función se dobla hacia abajo, entonces esta alcanza un punto máximo; por otra parte, si la función se dobla hacia arriba, entonces esta alcanza un punto mínimo.
Teorema de la segunda derivada
1.  , entonces
, entonces  alcanza un máximo local en
alcanza un máximo local en 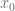 .
.
2. 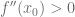 , entonces
, entonces  alcanza un mínimo local en.
alcanza un mínimo local en. 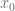
A continuación se mostrara un ejercicio para ejemplificar el criterio de primera derivada:
Teniendo la siguiente función:
En el segundo paso hallaremos la segunda derivada de la función la cual es:
En el tercer paso hallaremos los puntos críticos de la primera derivada:
Como podemos ver los puntos críticos son x= 1 y x= -1.
Ahora reemplazaremos estos puntos en la segunda derivada de nuestra función:
Finalmente reemplazaremos estos valores (1 y -1) en fx para obtener los valores de f(x) y finalmente vamos a graficar estos puntos en una grafica para verificar que nuestros cálculos sean correctos.
Como podemos observar en el punto (-1, 6) tenemos un punto máximo el cual decrece pasando por el punto de inflexión (0) y llegando hasta el punto ( 1,06) para finalmente decrecer.





0 Comentarios